By Kevin Aylward B.Sc.
Overview
This paper illustrates some example meme/gene competition effects.
Traits compete with each other. That is, one trait will attempt to use the resources or otherwise reduce the replication rates of other traits.
Basic Mathematics
It was noted in Replicator Theory that the basic equation for population increase is:
![]()
with solution
![]()
Where m = dM/dt, the number of mates in time t, q the quality, average number of offsprings per mate.
The immediate observation to this equation is that it predicts ever-increasing populations, which is clearly not observed in the long run, as populations obviously run out of resources. To make a first order correction to this a function is constructed such that as t increases to infinite, the population flattens out to a constant, but still retaining the same behavior at small t. From inspection, the following is seen to satisfy such conditions.
 - 1
- 1
Let Po/Pmx be very much smaller than 1. For small t:
![]()
For large t, the 1 can be neglected:
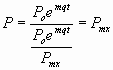
Thus the equation has the desired characteristics at small t and at large t, it is referred to as the Logistic function.
Differentiating equation 1, immediately results in the following differential equation
![]() - 2
- 2
Which is referred to as the Logistics equation of population growth, and produces an S type curve of population verses time.
Competition
Consider two populations of two different traits
![]() - 3
- 3
![]() - 4
- 4
Since it is assumed that traits compete for resources with each other, that is if one trait population increases, it will reduce the other traits population, the simplest modification can be made to the above set of equations.
![]() - 5
- 5
![]() - 6
- 6
That is, the population rates of each trait are reduced by a fraction of each competing population. These equations are called the Lotka-Volterra competition equations.
These equations can be simulated using standard Electronic Engineering Spice software such as SuperSpice. This technique is addressed in detail in other papers. A typical result is illustrated here:
Appendix
(work in progress and subject to error)
These papers may be freely copied only for non commercial use,
provided full credit is given to the author.
© Kevin Aylward 2003 - all rights reserved
Send comments or corrections to
kevin.aylwardEXTRACT@anasoft.co.uk
(remove EXTRACT from the email address)
Last updated 3td Dec 2003
Copyright © AnaSoft Ltd 1997-2002.
Published by AnaSoft. All rights reserved.